Year: 2025

Here is an app that simulates the interference pattern projected onto a wall or screen from an LED laser shining through 4 diffraction gratings.

Click on the below image of the app to run it in a separate window. I suggest trying a “Max Diffraction Order” of 2 (the bottom slider). The “Pair Rotation Angle” (top slider) can be anywhere from 0° to 90°. Values around 60° or so forn inages that look pretty cool to me. I especially like the way the image changes as you step through the angles 60°, 61°, 62°.

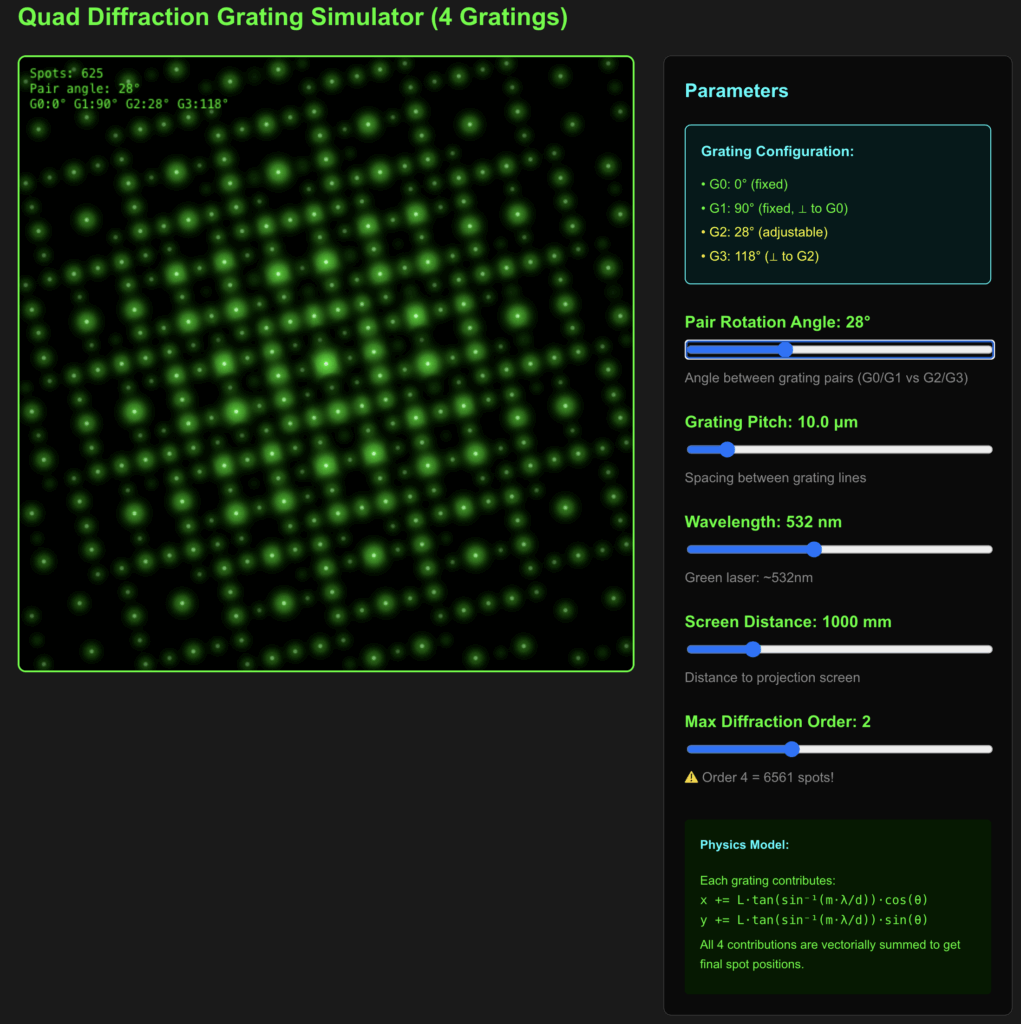
This laser interference pattern is similar to what would be produced by a Laser pointer’s beam passing through a diffraction grating – When you shine a laser pointer (green, 532nm wavelength) through a series of transmission diffraction gratings, you get a beautiful regular array of bright spots. The center spot is the zero-order (undiffracted beam), and the surrounding spots are the various diffraction orders. The symmetry and regularity of the pattern is characteristic of a diffraction grating pattern.

This simulation could be used as a demonstration setup for physics education – teaching about wave optics, interference and diffraction. It is a classic physics demonstration that beautifully illustrates the wave nature of light and the principles of diffraction.

Note that:

• The center spot is brightest (zero-order maximum)
• There’s symmetry in the pattern
• The spots gradually dim as you move away from center, but not in a trivial way
• It’s distinctly green (characteristic of common 532nm laser pointers)

The image produced (and simulated in the app) resembles a green laser pointer shining through a diffraction grating onto a screen or wall.

Here is a YouTube video of the app being used to interactively explore the effect of using various Rotation Angles between 0 and 90 degrees:

Additional detail:

The beam passes through 4 gratings (2 pairs of gratings), and the grating pairs are rotated relative to each other along the axis of the beam. I modeled this mathematically so I could simulate this spot pattern in software, providing the relative angle as input.

Modeling a multiple-grating system is a fascinating optics problem. The simulation accounts for both pairs of diffraction gratings and their relative rotation.

Dual Diffraction Grating Simulator

First I modeled an interactive simulator for dual-grating diffraction. Here’s how the mathematical model works:

Key Physics:

1. Each grating follows the diffraction equation:
   • sin(θ) = m·λ/d
   • Where m is the diffraction order (integers), λ is wavelength, d is grating pitch
2. Dual grating approach:
   • First grating creates diffraction orders in one direction
   • Second grating (rotated by angle α) creates its own diffraction pattern
   • Each spot from the first grating acts as a source for the second grating
   • Final pattern is the superposition of all combinations
3. Position calculation:
   • Each spot position combines contributions from both gratings
   • The second grating’s contribution is rotated by angle α
   • This creates the complex 2D patterns you observed

Try adjusting:

• Rotation angle (0-90°): Causes the pattern to evolve from a simple 1D grid (row of spots) to a 2D grid arrangement.
• Grating pitch: Changes the spacing between spots
• Max order: Controls how many diffraction orders are included

That simulator was a good start, but I wanted it to show more complex behavior like I’ve seen generated by a laser pointer I bought from a pawn shop several years ago. It appeared to me that there must be more going on with that actual laser pointer (see photos below) than just combining two gratings. So I made a guess that there are two pairs of gratings (4 gratings in total, in 2 groups of 2), and the first pair is rotated relative to the second pair.

Here is the laser pointer, sitting flat and then about to be mounted on a tri-pod:

And here (below) is the complex dot image projected on a wall. This is what originally inspired me to try and simulate it in software.

So in an effort to try and get this interesting behavior in software, I took the 2 grating model a step further, by using 4 gratings.

I’ll call the gratings G0, G1, G2 and G3.

• G0 and G1 are rotated 90 degrees relative to each other.
• G2 and G3 are rotated 90 degrees relative to each other.

The adjustable “angle” parameter now is the angle between these two pairs of gratings. This will hopefully create even more complex and beautiful interference patterns.

The simulator app as it is now uses 4 gratings. Here’s how it works:

Grating Configuration:

• G0 and G1: Fixed at 0° and 90° (perpendicular pair)
• G2 and G3: Rotated by the adjustable angle, also perpendicular to each other
• The angle slider controls the rotation between these two pairs

What the app shows:

• 0°: All gratings aligned in cardinal directions → square grid
• 22.5°: Interesting octagonal patterns
• 45°: More complexity with beautiful star/flower patterns
• Near 60°: maximum complexity (as I perceive it)
• 90°: Back to square grid (rotated)

The number of spots grows as (2·order+1)⁴, so be careful with high orders! Order 3 gives you 7⁴ or 2401 spots, which creates incredibly rich patterns, but performance may start to suffer and some unwelcome artifacts can make their way into the image.

Try sliding the angle slowly and watch how the pattern morphs – you should see fascinating symmetries emerge at different angles. This 4-grating setup creates much more complex and beautiful interference patterns than the 2-grating version.

© 2025 Muvicado Mindware LLC · Design and vision by Mark Barclay

Muvicado layout showcase

A muvicado layout is an arrangement of tiles that corresponds to a sequence of musical notes that can be performed easily, expressively, flexibly, and efficiently.

The song “Color My World“ is an example of such a layout. This song, by the classic horn band “Chicago“ from the early 80s I think, is a typical example of a Muvicado layout that illustrates and emphasizes the geometric nature of melody in a two dimensional space.

FACE the Music

The opening “F-A-C-E” (followed by CAFACECA…) was the initial inspiration for employing a visual 2D layout of musical notes for composing, arranging, performing and composing music – the original essence of Muvicado. The song starts with a simple piano arpeggio played in a vertical up/down gesture, moving along the left edge of the play area with the sequence of F, A, C, E – an arpeggiated Fmaj7.

Then, the melody progresses back down from E through C, A, F. Successive bars, with one or two notes changing between bars, progresses through the song from left to right, in roughly aligned columns of pads (for efficient navigation). At the end of the main theme, a “twiddle” is played, resolving to the root scale of Fmaj, ending the song, cycling around a small nested pad arrangement with the root major chord of Fmaj with a “9th” thrown in at the end as a farewell grace note.

The above basically describes the textbook “hello world” of a Muvicado layout.

Next. I’ll tighten this up and make it something that can be used as a reference and for demonstration purposes.

1. Formalizing “Muvicado layout”

Let’s pin this down:

A Muvicado layout is a 2D arrangement of playable tiles (pads, keys, nodes) where:

• A specific song or musical idea traces out simple geometric paths in that space
• Those paths are:
  • Performable (ergonomic for hands/fingers)
  • Expressive (invites phrasing, dynamics, voicings)
  • Flexible (easy to reharmonize / transpose / vary)
  • Efficient (minimal awkward jumps; reuse of shapes)
• And the geometry itself exposes or reinforces the underlying harmonic logic of the piece.

So instead of “notes scattered on keys,” you get:

• chords as vertical stacks,
• inversions as small shifts,
• voice leading as small geometric movements,
• fills and “twiddles” as orbits around a home cluster.

That’s Muvicado.

2. “Color My World” as a Muvicado archetype

Let’s look at this in layout terms (no sheet music, just geometry + pitch names):

1. Opening vertical gesture Left edge, straight line:
   • F – A – C – E → an Fmaj7 stack on a single column.
   • As a Muvicado move, that’s:
     • “Plant your hand here”
     • “This vertical is your home chord + color (maj7).”
   • Visually: a tall, elegant column. It teaches the hand the chord.
2. Mirror / inversion descent Then you describe:
   • moving from E through C – A – F:
     • same four chord tones, reversed order.
     • Geometrically: a downward traversal of the same column or a flip/inversion path.
   • Muvicado-wise:
     • This is the concept of shape-preserving motion.
     • “You are still inside Fmaj7-land; you’re just re-threading its tones.”
3. Progressing left → right, one bar at a time Key property you called out:
   • Successive bars only change one or two notes.
   • On a grid, that looks like:
     • Each bar = a vertical slice (column group).
     • Changes = tiny shifts (one tile over / up / down).
   • This is visible voice-leading:
     • Harmonies glide.
     • The player feels: “stay in the neighborhood; only nudge one finger.”
   • That’s what Muvicado is about:
     • Efficient.
     • Easy to learn.
     • Geometrically memorable.
4. The “twiddle” + F major + 9th resolution End of the main theme:
   • A compact little nested pad cluster: tones of F major plus the 9th (G).
   • A small circular or diamond-shaped orbit pattern.
   • Final G (9th) as a gentle grace-note goodbye.
   • In layout language:
     • “Here is your home base motif: a tight cluster you can swirl around.”
     • So we’ve encoded:
       • tonic,
       • color tone (9),
       • resolution behavior,
         into a tiny local geometry.

“Color My World” behaves like:

• Column (Fmaj7 identity)
• → Local flips/shifts (minimal-move variations)
• → Rightward drift (song form unfolding)
• → Nested home cluster (resolution pad).

It’s an examplke of using a visual pattern language for musical ideas.

3. One concrete way to sketch it…

Here’s a partial illustrative pad map that has been prototyped (not literal to every note; it encodes the concept):

(col 0)     (col 1)     (col 2)     (col 3)
  E           E           E           G
  C           C           D           F
  A           A           A           C
  F           F           F           F

• Col 0: pure F–A–C–E vertical → “Here’s your Fmaj7.”
• Cols 1–2: small tweaks (e.g., D appears, voicings shift) → voice-leading geometry.
• Col 3: tight F–A–C–G cluster → Fadd9 / Fmaj9 “twiddle zone.”

The performer would play:

• mostly vertical + tiny diagonals,
• almost no ugly leaps,
• always “seeing” the harmonic neighborhood.

That’s a Muvicado layout: a performance surface where the song is a clean geometric walk.

4. This is central to Muvicado as a platform

“Color My World” is my first example of a “visual musical story”:

• It shows that:
  • A well-designed grid can encode a whole tune as a shape, not just as pitches.
  • Beginners can literally trace the path.
  • Advanced players can decorate inside the same geometry (altered extensions, reharm, rhythmic variation) without getting lost.
• We can provide an illustrative demo:
  • Show the F–A–C–E column.
  • Show tiny bar-to-bar changes.
  • Show the end “twiddle cluster.”
  • This will illustrate how Muvicado layouts let you design instruments so songs live as shapes.

Next, we’ll derive a generalized rule set: how to detect / construct Muvicado-friendly layouts from any chord progression, turning “Muvicado layout” into a rule set that can be applied to any chord progression.

We’ll split this into two things:

1. How to construct a Muvicado-friendly layout from chords.
2. How to detect when a layout is Muvicado-friendly.

Hopefully, this can stand-in as a usable spec.

1. Core idea (what we’re optimizing for)

A Muvicado layout is good when a song’s notes form:

• Smooth paths (small moves, repeatable shapes)
• Clear geometry (lines, clusters, orbits you can see and remember)
• Consistent interval vectors (a 3rd, 4th, etc. “feels” like the same move everywhere)
• Ergonomic play (hands don’t jump stupid distances)
• Expressive flexibility (easy to add chord tones, extensions, fills without leaving the local geometry)

We’re encoding music as navigation on a 2D grid.

So the rule set is basically: given a chord progression + key center, choose a mapping and note layout that makes that navigation beautiful.

2. Construction Rules (from chord progression → layout)

Think of this as a design/algorithm you could implement.

Step 0 — Choose a lattice

Pick a 2D pitch-mapping scheme that’s consistent:

Examples. These may be swapped depending on the instrument (selected by per-pad MIDI channel):

• Vertical = chord tones stacked by 3rds, horizontal = time/sections.
• Or: vertical = scale degree, horizontal = 4ths/5ths.
• Or: one axis = diatonic steps, other axis = chromatic or function.

Rule C0: Whatever you choose, the same interval should correspond to the same geometric move (or small set of moves) everywhere.

Step 1 — Anchor the “home” chord cluster

Given:

• Key center K (e.g., F)
• Primary chord(s) (I, i, or tonic-ish)

Rules:

1. Place the tonic chord (e.g., F–A–C–E) as a compact, readable shape:
   • Often a vertical or diagonal stack.
   • This becomes your Home Column / Home Cluster.
2. Ensure:
   • Root is easy to hit,
   • Color tones (7, 9, 6) are nearby (adjacent tiles, not across the map).

This is the “Color My World” Fmaj7 column generalized.

Step 2 — Layout for voice-leading, not just chords

For each chord change in the progression:

Given:

• Previous chord: $C_n$Cn​
• Next chord: $C_{n+1}$Cn+1​
• Shared tones: $C_n \cap C_{n+1}$Cn​∩Cn+1​
• Moving tones: $C_{n+1} \setminus C_n$Cn+1​∖Cn​

Rules (VL-series):

• VL1: Shared tones should:
  • stay on the same tiles if possible,
  • or move by 1 step (up/down/diagonal).
• VL2: Moving tones should:
  • move by small geometric steps (ideally 1–2 tiles).
• VL3: Avoid mappings where a simple ii–V–I or I–vi–IV–V requires wild zigzags.

In code terms, for each chord transition, we want to minimize total tile-distance of voices.

Step 3 — Bars and sections as columns / lanes

For progressions across time:

• Treat each bar or harmonic event as a vertical slice (or small region).
• Chords in chronological order move left → right (or another consistent direction).

Rules (T-series):

• T1: The main melody path should read as a mostly monotonic path along one axis (e.g., left→right) with gentle vertical/diagonal moves.
• T2: Harmony/voicing for each bar sits close to the previous bar’s voicing:
  • At most 1–2 tiles away for most inner voices.
• T3: Repeated sections reuse the same or congruent shapes (so A section feels like a recognizable pattern).

This is what makes the layout “geometric” instead of random.

Step 4 — Twiddle zones and color tones

For fills, runs, and expressive stuff:

Rules (X-series):

• X1: Around each primary chord, define a local neighborhood (e.g. radius-1 or radius-2 tiles) containing:
  • scale tones,
  • chord extensions (9, 11, 13),
  • neighbor tones.
• X2: Ensure twiddles (grace notes, neighbor movements, turns) form small closed loops or arcs:
  • visually: tiny orbits, diamonds, triangles.
• X3: The tonic/home twiddle zone should be:
  • especially tight and inviting (your “end of Color My World” vibe),
  • easy to noodle on without leaving key.

This is how we “bake in” safe improvisation.

Step 5 — Cross-check ergonomics & efficiency

Now let’s treat the pad layout as something to score.

For a given song mapped to a grid view of the notes in a song , compute:

1. Path length: sum of distances between successive melody notes.
2. Max jump: largest single movement.
3. Chord reuse: how many notes stay on same tiles / close tiles between chords.
4. Locality: proportion of notes inside local neighborhoods of main clusters.
5. Shape coherence: does the path look like a few simple motifs (lines, arcs, orbits)?

Rule E1: A layout is “Muvicado-friendly” if:

• Average step size is small,
• Max jumps are rare,
• Voice leading is visually obvious,
• The song’s main motives are drawable as simple geometric gestures.

(We could later formalize that as a cost function and search for an optimal mapping)

3. Detection Rules (given a layout + tune: is it Muvicado?)

Given:

• A fixed grid layout,
• A mapping from notes → pads,
• A specific chord progression + melody.

Check:

1. Interval Consistency
   • Same musical intervals correspond to the same or similar geometric moves.
   • If a major 3rd is sometimes near, sometimes miles apart, that’s a red flag.
2. Voice-Leading Smoothness
   • Track each voice (or implied inner voice).
   • Are changes between chords:
     • mostly 0–1 tile moves? ✔
     • often 3+ tiles jumps for no harmonic reason? ✘
3. Melodic Path Geometry
   • Plot the melody on the grid.
   • Does it form:
     • lines / arcs / mirrored shapes / small repeated motifs? ✔
     • or noisy random scatter? ✘
4. Local Neighborhood Richness
   • Around tonic and key chords:
     • Are chord tones + key scale tones clustered? ✔
     • Or weirdly sparse / fragmented? ✘
5. Playability
   • For two human hands:
     • Are most notes within a natural reach span?
     • Can common voicings be held without contortion?

If a layout scores well on those, we could call it a valid Muvicado layout for that tune.

© 2025 Muvicado Mindware LLC · Design and vision by Mark Barclay

We like to tell ourselves that good ideas arrive in lightning flashes.

A walk in the woods. A shower. A late-night scribble on a napkin. The myth is that creativity appears out of nowhere — a pure bolt from the blue.

But if we’re honest, most of what we call “original” is something quieter and more humble: we’re thinking between the shoulders of giant minds.

The giants metaphor is a familiar one. It suggests that we’re lifted up by those who came before us — scientists, artists, teachers, mentors, friends — and from that higher vantage point we can see further. That image is beautiful and true, but it’s also a bit misleading. It’s too clean. Too solitary.

Real thinking doesn’t just happen on someone’s shoulders, looking out at the horizon. It happens between minds — ours and theirs. In the spaces where ideas echo, collide, blend, and cross-pollinate.

The myth of the lone genius

Every field has its heroes: the one composer, the one inventor, the one mathematician, the one visionary founder who “changed everything.”

But look more closely and you’ll always find a network:

• A teacher who asked the right question at the right time.
• A forgotten paper that introduced a small twist nobody noticed at first.
• A colleague who argued with you just enough to make you sharpen your thinking.
• A book you read as a teenager that quietly rewired the way you see the world.

By the time an idea surfaces in your notebook or in your prototype, it has already flowed through decades or centuries of other people’s work. You’re not stealing from them. You’re participating in the same ongoing conversation they were part of.

We don’t invent from scratch. We tune. We combine. We rearrange. We question. We repair. We remix.

That’s what it means to think between the shoulders of giant minds.

The invisible lineage behind your ideas

If you trace any one of your current projects backwards, you’ll almost always find an invisible lineage.

Maybe your way of organizing information came from that one meticulous teacher who color-coded everything on the board.
Maybe your curiosity about patterns came from early puzzles, board games, or the weird joy of discovering that math could be playful.
Maybe your interest in human-friendly tools came from watching someone struggle with brittle, unfriendly software and thinking: “It doesn’t have to be this way.”

A lot of what we call “inspiration” is really this: a quiet, accumulated pressure of prior minds nudging us toward our own version of the work.

And here’s the important part: acknowledging that doesn’t make your contribution smaller. It makes it more human.

You’re not a fraud because your ideas have ancestors. You’re part of a lineage because they do.

Few ideas are truly unborrowed

You could phrase it bluntly: Few ideas are not accidentally borrowed.

We absorb more than we realize: from articles, open-source repositories, conversations, half-remembered talks, even casual comments that stick in our minds years later. Most of the time, the lines of influence are so tangled that we couldn’t untangle them even if we tried.

That doesn’t mean rigor and attribution don’t matter — they do. It just means that, on a deeper level, creativity has always been a shared endeavor.

We’re all building with pieces we didn’t forge ourselves. What matters is:

• How honestly we work.
• How clearly we acknowledge the foundations when we’re aware of them.
• How generously we share what we discover so someone else can build on us.

We inherit, transform, and pass it on.

Thinking as a relay, not a spotlight

Once you start seeing thinking as a relay instead of a spotlight, a few things change:

• Pressure drops. You no longer need to be the once-in-a-century genius. You just need to carry the baton well for your leg of the race.
• Curiosity rises. Instead of obsessing over “being original,” you can ask better questions: What am I standing on? What am I extending? What can I repair or connect that others haven’t?
• Gratitude grows. You begin to notice how many people — some you’ve never met — quietly invested in the tools, ideas, and patterns you now take for granted.

You realize that the real miracle is not that you had an idea, but that so much infrastructure of thought was already there waiting for you to notice it.

The responsibility of being someone else’s “giant”

There’s also a gentle responsibility baked into this metaphor.

If we are, all of us, thinking between the shoulders of giant minds, then we are also, in small ways, becoming shoulders for someone else.

Not necessarily through world-famous achievements. Sometimes through:

• A clean explanation that finally makes a tricky concept feel intuitive.
• An open, generous tool or library that saves someone else days of frustration.
• A blog post or talk that gives another person permission to explore their own weird ideas.
• A game, puzzle, or visualization that quietly plants a seed of curiosity.

You may never know whose work your work enables. But that doesn’t make the influence less real.

Every time you turn your private insights into something visible — a sketch, a prototype, a post, a talk, a little app, a tiny utility script — you’re adding a small but sturdy foothold to the mountain of shared understanding.

Somewhere, someone may stand on it. Or think between it and a dozen others, and create something you could never have imagined.

A more honest, kinder story of creativity

“We think between the shoulders of giant minds” is, in a way, an invitation to a kinder story about creativity:

• Kinder to the past, because it recognizes how much we owe.
• Kinder to ourselves, because it takes the crushing weight of “be utterly original” off our shoulders.
• Kinder to the future, because it reminds us that our work can be a gift, not just a product.

So the next time an idea appears and you’re tempted to dismiss it as “not original enough,” try a different lens:

Ask instead:

• Which minds am I standing between right now?
• What small, honest contribution can I add to this ongoing conversation?
• How can I leave this idea in better shape than I found it?

You don’t have to be the giant.

You just have to be part of the bridge between them.

Meta-note: This essay was generated with the help of an AI assistant (ChatGPT), using my prompt and prior conversations as raw material. I’ve reviewed it, resonated with it, and chosen to share it here as part of my ongoing exploration of human + machine co-writing.

Thought I’d take a look at React.JS today, as it seems to share parts of the underpinnings of Kotlin @Compose.

With ChatGPT’s guidance, it was remarkable easy to put together a basic REACT app that runs statically from an AWS S3 bucket, using only the Linux command line. In the bash shell it only took about 5 minutes once I had the content in the chat available.

Click the image below to run the simple app…

I was also pleasantly surprised how well the markdown text copied from the ChatGPT session formatted into a WordPress web page.

(see the session)

3 densely inspiring days of indulgence in two of my passions, Math and Music

This week (WTC[{“We”},{“Th”},{“Fr”}]), I was moved to action by the excellent presentations and “After Hours” sessions.

First, Stephen’s keynote address was thoughtful, relevant and positive (a welcome perspective of the current state of things). In the last part of his keynote, he really made me re-think my long-time habit of staying in the cozy comfort zone of writing almost all my own low level code (in other great languages). That was something that resonated with me and reminded me of the benefits of coding at a higher level. The Wolfram language and the Mathematica notebook environment frees you of as much of the low-level struggle as can be hoped for (and it’s still fun!)

Watch to the keynote:

TheInnovator award winners list some pretty impressive contributions.

Here’s a link to a recent post introducing this year’s Innovator Award Winners. on Danielle Mayer’s blog.

And among all the great sessions I attended that took place throughout the week, my favorite was the presentation that links the environment to music creation tools…

Introducing Symbolic Music in Wolfram Language

Speakers: Carlo Giacometti, Rebecca Frederick
Handle notes, voices, scores and more in Wolfram Language: get a glimpse into what’s coming for symbolic music in the next release!

I’m not sure if the session is available yet as a public link, but I suspect it will be available in Wolfram MathWorld or somewhere soon.

Content in this talk happens to align nicely with the Muvicado concept in several (just to name a few) ways.

I can’t wait to start using some of these:

• Import[] of MIDI files
• Wolfram APIs for MIDI interfacing
• audio rendering of MIDI sequences
• SoundNote[]
• MusicVoice[]
• MusicNote[]
• MusicScore[]
• MusicPlot[]
• MusicRest[]
• MusicTimeSignature[]
• MusicKeySignature[]
• MusicChord[]
• MusicInterval[“PerfectFifth”]
• MusicNoteDuration[]
• MusicNotePitch[]
• MusicMeasure[]
• MusicXML. MEI, MNX

The future directions of these music-related WL features are quite promising!

And Mathematica is now my most fun single tool to use.

I’ll be attending the 3-day Wolfram Virtual Technology Conference 2025. I hope to learn more powerful Mathematica features to support my recreational math interests in areas such as Graph Theory, Combinatorics and more.